第7章 線形システムの分析

動学的マクロ経済モデルの典型的なパターンは, 均衡経路の拘束条件をストック変数に関する初期条件と, 価格に関する終端条件 (横断性条件) で与えるというものである. ストックは過去の経済活動によって定まるため過去の情報から決定される (先決変数). 一方, 価格は将来価値を反映して決まるものなので, 未来の情報を用いて決定される (非先決変数). したがって, 経済モデルは時間の流れに沿って決まっていく成分と, 時間の流れを逆行して決まる成分が組み合わさって成り立っているのが普通である. ゆえに経済モデルの解析は線形システムであっても比較的複雑なものになる. 基本モデルの解法をきちんと理解しておくことは大変重要である.

本稿では, Blanchard and Kahn (1980) および Klein (2000) の決定論バージョンを考察しよう25。具体的には, ジョルダン標準形およびワイエルシュトラス標準形を用いた分析を確率的な要因が一切存在しないモデルに対して適用する. 確率的な要因を入れたモデルでも基本的な考え方は変わらないので, ここでの分析手法をよく理解してほしい. 条件付き期待値のルールを一通り理解すれば確率的なモデルに容易に拡張できる.

ただし, すでに指摘した通り, ジョルダン標準形やワイエルシュトラス標準形は数値計算では通常用いることができない. 固有値の重複度に関して浮動小数点数を用いた判定が難しいからである. この問題はSchur 分解や QZ 分解あるいは特異値分解を利用することで解決するのであるが, それは次回以降に譲って理論的な結果をまず見てみよう.

7.1 行列公式

本題に入る前にいくつかの行列公式をまとめておこう.

7.1.1 逆行列公式

本稿の計算結果を既存研究の結果と比較すると (記号の違いという明白な相違点以外にも) 見かけ上異なる解を得ていることが分かるだろう. これは導出方法が異なるために発生した見せかけの違いであって本質的なものではない. 文献と比較する際には次の行列公式を念頭においておくとよい.
定理 7.1 \(A,B,C,D\) は適当な次元の行列であるとする. \(A\) および \(D-CA^{-1}B\) を正則とする. このとき\(\left[\begin{smallmatrix}A & B\\ C & D \end{smallmatrix}\right]\) は正則であり, 次式が成立する. \[ \begin{bmatrix}A & B\\ C & D \end{bmatrix}^{-1}=\begin{bmatrix}A^{-1}+A^{-1}B(D-CA^{-1}B)^{-1}CA^{-1} & -A^{-1}B(D-CA^{-1}B)^{-1}\\ -(D-CA^{-1}B)^{-1}CA^{-1} & (D-CA^{-1}B)^{-1} \end{bmatrix}. \]

系 7.1 \(A,C,D\) は適当な次元の行列であるとする. \(A\) および \(D\) を正則とする. このとき\(\left[\begin{smallmatrix}A & 0\\ C & D \end{smallmatrix}\right]\) は正則であり, 次式が成立する. \[ \begin{bmatrix}A & 0\\ C & D \end{bmatrix}^{-1}=\begin{bmatrix}A^{-1} & 0\\ -D^{-1}CA^{-1} & D^{-1} \end{bmatrix}. \]

定理7.1 および系@ref{cor:blockcor}を証明せよ.

7.1.2 シルベスタ方程式

2つの演算を定義しよう. 行列の各列を縦に積み上げる写像を \(\mathrm{vec}:\mathbb{F}^{m\times n}\to\mathbb{F}^{mn}\) と書く. すなわち, \[ \begin{aligned} \mathrm{vec}\left(\begin{bmatrix}a_{11} & \cdots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{m1} & \cdots & a_{mn} \end{bmatrix}\right)=\begin{bmatrix}a_{11} & \cdots & a_{m1} & \cdots & \cdots & a_{1n} & \cdots & a_{mn}\end{bmatrix}^{\top}. \end{aligned} \] 容易に分かることだが, \(\mathrm{vec}\) は線形写像である.

\(A\in\mathbb{F}^{m\times n}\) と \(B\in\mathbb{F}^{p\times q}\) のクロネッカー積 \(A\otimes B\in\mathbb{F}^{mp\times nq}\) を \[ A\otimes B:=\begin{bmatrix}a_{11}B & \cdots & a_{1n}B\\ \vdots & \ddots & \vdots\\ a_{m1}B & \cdots & a_{mn}B \end{bmatrix} \] によって定義する. 次の補題を証明しよう.
補題 7.1 \(A\), \(B\), \(C\) を適当なサイズの行列とする. このとき, \(\mathrm{vec}(ABC)=(C^{\top}\otimes A)\mathrm{vec}(B)\) が成り立つ.

証明. \(A\in\mathbb{F}^{m\times n}\), \(B\in\mathbb{F}^{n\times p}\), \(C\in\mathbb{F}^{p\times q}\) とする. \(B=\begin{bmatrix}B_{1} & \cdots & B_{p}\end{bmatrix}\), \(C=\begin{bmatrix}C_{1} & \cdots & C_{q}\end{bmatrix}\)とすれば \[ \begin{aligned} \left(C^{\top}\otimes A\right)\mathrm{vec}(B) & =\begin{bmatrix}c_{11}A & \cdots & c_{p1}A\\ \vdots & \ddots & \vdots\\ c_{1q}A & \cdots & c_{pq}A \end{bmatrix}\begin{bmatrix}B_{1}\\ \vdots\\ B_{p} \end{bmatrix}=\begin{bmatrix}c_{11}AB_{1}+\cdots+c_{p1}AB_{p}\\ \vdots\\ c_{1q}AB_{1}+\cdots+c_{pq}AB_{p} \end{bmatrix}\\ & =\begin{bmatrix}\begin{bmatrix}AB_{1} & \cdots & AB_{p}\end{bmatrix}C_{1}\\ \vdots\\ \begin{bmatrix}AB_{1} & \cdots & AB_{p}\end{bmatrix}C_{q} \end{bmatrix}=\begin{bmatrix}ABC_{1}\\ \vdots\\ ABC_{q} \end{bmatrix}=\mathrm{vec}(ABC). \end{aligned} \]

定理 7.2 (離散時間シルベスタ方程式) \(A\), \(B\), C を適当なサイズの行列, \(I-\left(B^{\top}\otimes A\right)\) は正則であるとする. 行列方程式 \(AXB-X+C=0\)の解 \(X\) は, \[ \mathrm{vec}(X)=\left[I-\left(B^{\top}\otimes A\right)\right]^{-1}\mathrm{vec}(C) \] によって与えられる.

証明. 全体を \(\mathrm{vec}\) で写して, \(\mathrm{vec}(AXB)-\mathrm{vec}(X)+\mathrm{vec}(C)=0\)を得る. 補題 7.1 より\(\left(B^{\top}\otimes A\right)\mathrm{vec}(X)-\mathrm{vec}(X)=-\mathrm{vec}(C)\). したがって, \(\mathrm{vec}(X)=\left[I-\left(B^{\top}\otimes A\right)\right]^{-1}\mathrm{vec}(C)\).

7.2 \(E=I\) のケース

無限期間のシステム方程式 \(Ex_{t+1}=Ax_{t}+Bu_{t}\) において \(E=I\) なるケースを考える. すなわち, \[\begin{equation} x_{t+1}=Ax_{t}+Bu_{t},\quad t=0,1,\dots,\tag{7.1} \end{equation}\] 各ベクトルと行列のサイズは \(x\in\mathbb{R}^{n}\), \(u\in\mathbb{R}^{m}\), \(A\in\mathbb{R}^{n\times n}\), \(B\in\mathbb{R}^{n\times m}\) とする. \(u\) は外生的に与えられるショックである. 序文に述べた通り, \(x\) を構成する変数の一部に初期条件が与えられている状況を想定している. 具体的には変数 \(x\) が \(x^{1}\in\mathbb{R}^{n_{1}}\) および \(x^{2}\in\mathbb{R}^{n_{2}}\) によって \[\begin{equation} x_{t}=\begin{bmatrix}x_{t}^{1}\\ x_{t}^{2} \end{bmatrix} \tag{7.2} \end{equation}\] と記述でき, 初期条件が \[ x_{0}^{1}=\bar{x}_{0}^{1}, \] で与えられているとする. 終端条件として経路の発散スピードが幾何数列の発散スピードを超えないことを仮定する. すなわち, 任意の \(-1<\rho<1\) について \[\begin{equation} \lim_{T\to\infty}\rho^{T}\|x_{T}\|=0 \tag{7.3} \end{equation}\]

が成り立つ \(x\) を実行可能な解であるとする. 式 (7.1) を式 (7.2) に適合するようにブロック行列表現すると

\[ \begin{bmatrix}x_{t+1}^{1}\\ x_{t+1}^{2} \end{bmatrix}=\begin{bmatrix}A_{11} & A_{12}\\ A_{21} & A_{22} \end{bmatrix}\begin{bmatrix}x_{t}^{1}\\ x_{t}^{2} \end{bmatrix}+\begin{bmatrix}B_{1}\\ B_{2} \end{bmatrix}u_{t} \] と書ける. \(A\) のジョルダン分解 \[ \begin{bmatrix}A_{11} & A_{12}\\ A_{21} & A_{22} \end{bmatrix}=P\begin{bmatrix}J_{s} & 0\\ 0 & J_{u} \end{bmatrix}P^{-1} \] に基いて状態方程式(7.1)を変形し, \[ P^{-1}\begin{bmatrix}x_{t+1}^{1}\\ x_{t+1}^{2} \end{bmatrix}=\begin{bmatrix}J_{s} & 0\\ 0 & J_{u} \end{bmatrix}P^{-1}\begin{bmatrix}x_{t}^{1}\\ x_{t}^{2} \end{bmatrix}+P^{-1}\begin{bmatrix}B_{1}\\ B_{2} \end{bmatrix}u_{t} \] を得る. \(P\) をうまく選んで, \(J_{s}\) の対角成分には絶対値が1以下の固有値, \(J_{u}\) の対角成分には絶対値が \(1\) より大きい固有値が並んでいるとしよう. この結果, \(J_{u}\) は正則になる. \(y:=P^{-1}x\), \(C:=P^{-1}B\) と変数変換することで

\[\begin{equation} \begin{bmatrix}y_{t+1}^{s}\\ y_{t+1}^{u} \end{bmatrix}=\begin{bmatrix}J_{s} & 0\\ 0 & J_{u} \end{bmatrix}\begin{bmatrix}y_{t}^{s}\\ y_{t}^{u} \end{bmatrix}+\begin{bmatrix}C_{s}\\ C_{u} \end{bmatrix}u_{t} \tag{7.4} \end{equation}\]

を得る. ただし, \[ y^{s}\in\mathbb{R}^{n_{s}},\ y^{u}\in\mathbb{R}^{n_{u}} \] であり, 行列, およびその各ブロックはすべて適合するサイズをもつものとする.

典型的なケースでは初期条件の数が変数の次元に対して不足しているため, 最終期までの情報を使って不足した \(t=0\) 時点の条件を補ってから解を決定する. やや天下り的ではあるが, 式(7.4) 下段のシステムを, \(t\) 期から \(T\) 期までの情報を使って後ろ向きに (forward-looking に) 解いてみよう26。

\[\begin{align} y_{t}^{u} & =J_{u}^{-1}y_{t+1}^{u}-J_{u}^{-1}C_{u}u_{t}\nonumber \\ & =J_{u}^{-1}\left(J_{u}^{-1}y_{t+2}^{u}-J_{u}^{-1}C_{u}u_{t+1}\right)-J_{u}^{-1}C_{u}u_{t}\nonumber \\ & =J_{u}^{-2}\left(J_{u}^{-1}y_{t+3}^{u}-J_{u}^{-1}C_{u}u_{t+2}\right)-J_{u}^{-2}C_{u}u_{t+1}-J_{u}^{-1}C_{u}u_{t}\nonumber \\ & =J_{u}^{-3}y_{t+3}^{u}-J_{u}^{-3}C_{u}u_{t+2}-J_{u}^{-2}C_{u}u_{t+1}-J_{u}^{-1}C_{u}u_{t}\nonumber \\ & =\cdots\nonumber \\ & =J_{u}^{t-T}y_{T}^{u}-\sum_{k=0}^{T-t-1}J_{u}^{-k-1}C_{u}u_{t+k}. \tag{7.5} \end{align}\]

ここで, \(J_{u}^{-1}\) は安定行列であり, \(T\to\infty\) のとき幾何数列のオーダーで減衰する. 一方 \(y_{T}^{u}\) は \(x_{T}\) の1次結合であるから, 仮定(7.3)により\(\lim_{T\to\infty}\|J_{u}^{t-T}y_{T}^{u}\|=0\). つまり,

\[\begin{equation} y_{t}^{u}=-\sum_{k=0}^{\infty}J_{u}^{-k-1}C_{u}u_{t+k} \tag{7.6} \end{equation}\]

が成り立つ.27

変数 \(x\) と \(y\) の関係から任意の \(t\) に対して \[\begin{equation} \begin{bmatrix}x_{t}^{1}\\ x_{t}^{2} \end{bmatrix}=P\begin{bmatrix}y_{t}^{s}\\ y_{t}^{u} \end{bmatrix}=\begin{bmatrix}P_{1s} & P_{1u}\\ P_{2s} & P_{2u} \end{bmatrix}\begin{bmatrix}y_{t}^{s}\\ y_{t}^{u} \end{bmatrix} \tag{7.7} \end{equation}\] が成り立つ. \(t=0\) したとき, (7.7) に現れる変数の内 \(x_{0}^{1}=\bar{x}_{0}^{1}\) と \(y_{0}^{u}=\bar{y}_{0}^{u}\) が定まっている. ここで, \(P_{1s}\in\mathbb{R}^{n_{1}\times n_{s}}\), \(P_{1u}\in\mathbb{R}^{n_{1}\times n_{u}}\), \(P_{2s}\in\mathbb{R}^{n_{2}\times n_{s}}\) および \(P_{2u}\in\mathbb{R}^{n_{2}\times n_{u}}\) に注意せよ. この情報から, \(x_{0}^{2}\) および \(y_{0}^{s}\)を決定できれば解軌道が完全に定まる. \(t=0\) で成立する線形方程式 \[\begin{align} \bar{x}_{0}^{1} & =P_{1s}y_{0}^{s}+P_{1u}\bar{y}_{0}^{u} \tag{7.8}\\ x_{0}^{2} & =P_{2s}y_{0}^{s}+P_{2u}\bar{y}_{0}^{u}\tag{7.9} \end{align}\] を変形し, 未知量 \((x_{0}^{2},y_{0}^{s})\) に関する次の線形方程式を得る. \[\begin{equation} \begin{bmatrix}P_{1s} & 0\\ P_{2s} & -I_{n_{2}} \end{bmatrix}\begin{bmatrix}y_{0}^{s}\\ x_{0}^{2} \end{bmatrix}=\begin{bmatrix}I_{n_{1}} & -P_{1u}\\ 0 & -P_{2u} \end{bmatrix}\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{u} \end{bmatrix}.\tag{7.10} \end{equation}\]

ベクトルと行列のサイズはそれぞれ \[ \begin{bmatrix}y_{0}^{s}\\ x_{0}^{s} \end{bmatrix}\in\mathbb{R}^{n_{s}+n_{2}},\quad\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{u} \end{bmatrix}\in\mathbb{R}^{n_{1}+n_{u}}, \]

\[ \Pi_{1}:=\begin{bmatrix}P_{1s} & 0\\ P_{2s} & -I \end{bmatrix}\in\mathbb{R}^{n\times(n_{s}+n_{2})},\quad\Pi_{2}:=\begin{bmatrix}I & -P_{1u}\\ 0 & -P_{2u} \end{bmatrix}\in\mathbb{R}^{n\times(n_{1}+n_{u})}. \] 解の決定に際して, 3つの場合に場合分けをする.

\(n_{s}+n_{2}>n\)

\[ n_{s}+n_{2}>n=n_{1}+n_{2}\Longleftrightarrow n_{s}>n_{1} \] が成り立つとすれば, 方程式 (7.10) の係数行列 \(\Pi_{1}\in\mathbb{R}^{n\times(n_{s}+n_{2})}\) は横長の行列である. したがって, 方程式 (7.10) を満たす \((y_{0}^{s},x_{0}^{2})\) は無数に存在する. 解軌道が無数に存在するので解は不決定 (indeterminate)であるという. 一般に, 初期値の選び方に自由度がある場合に不決定性があるという.

\(n_{s}+n_{2}<n\)

\[ n_{s}+n_{2}<n=n_{1}+n_{2}\Longleftrightarrow n_{s}<n_{1} \] が成り立つとしよう. このとき, 係数行列 \(\Pi_{1}\) は縦長の行列であるから, 方程式 (7.10) を満たす \((y_{0}^{s},x_{0}^{2})\) は一般には存在しない. 解の存在を保証するためには, \[ \Pi_{2}\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{u} \end{bmatrix}\in\mathrm{im}\Pi_{1} \] となるように初期条件と入力を決めなければならない.

\(n_{s}+n_{2}=n\)

最後に

\[ n_{s}+n_{2}=n=n_{1}+n_{2}\Longleftrightarrow n_{s}=n_{1} \] が成り立つとしよう. このとき, \(\Pi_{1}\) は正方行列である. さらにこれが正則であれば解 \((y_{0}^{1},x_{0}^{2})\) が一意的に定まる. \(\det\Pi_{1}=\det P_{1s}\) より, \(\Pi_{1}\) の正則性は \(P_{1s}\) の正則性と同値である. \(P_{1s}\) が正則でない場合は再び解の不決定性が現れる. 系7.1 より\(P_{1s}\) が正則であれば \[ \Pi_{1}^{-1}=\begin{bmatrix}P_{1s}^{-1} & 0\\ P_{2s}P_{1s}^{-1} & -I \end{bmatrix}. \] したがって, \[ \begin{aligned} \begin{bmatrix}y_{0}^{s}\\ x_{0}^{2} \end{bmatrix} & =\begin{bmatrix}P_{1s}^{-1} & 0\\ P_{2s}P_{1s}^{-1} & -I \end{bmatrix}\begin{bmatrix}I & -P_{1u}\\ 0 & -P_{2u} \end{bmatrix}\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{u} \end{bmatrix}\\ & =\begin{bmatrix}P_{1s}^{-1} & -P_{1s}^{-1}P_{1u}\\ P_{2s}P_{1s}^{-1} & P_{2u}-P_{2s}P_{1s}^{-1}P_{1u} \end{bmatrix}\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{u} \end{bmatrix} \end{aligned} \] によって \(t=0\) における変数値が完全に決定される. この等式は任意の \(t=0\) 以外でも成り立つことに注意をしておく. \[ \begin{aligned} \begin{bmatrix}y_{t}^{s}\\ x_{t}^{2} \end{bmatrix} & =\begin{bmatrix}P_{1s}^{-1} & -P_{1s}^{-1}P_{1u}\\ P_{2s}P_{1s}^{-1} & P_{2u}-P_{2s}P_{1s}^{-1}P_{1u} \end{bmatrix}\begin{bmatrix}x_{t}^{1}\\ y_{t}^{u} \end{bmatrix} \end{aligned} \] この関係を使って, 次の方程式を得る. \[\begin{align} \begin{bmatrix}x_{t+1}^{1}\\ x_{t+1}^{2} \end{bmatrix} & =P\begin{bmatrix}y_{t+1}^{s}\\ y_{t+1}^{u} \end{bmatrix}\nonumber \\ & =\begin{bmatrix}P_{1s} & P_{1u}\\ P_{2s} & P_{2u} \end{bmatrix}\begin{bmatrix}J_{s}\\ & J_{u} \end{bmatrix}\begin{bmatrix}y_{t}^{s}\\ y_{t}^{u} \end{bmatrix}+Bu_{t}\nonumber \\ & =\begin{bmatrix}P_{1s} & P_{1u}\\ P_{2s} & P_{2u} \end{bmatrix}\begin{bmatrix}J_{s}\\ & J_{u} \end{bmatrix}\begin{bmatrix}P_{1s}^{-1}x_{t}^{1}-P_{1s}^{-1}P_{1u}y_{t}^{u}\\ y_{t}^{u} \end{bmatrix}+Bu_{t}\nonumber \\ & =\begin{bmatrix}P_{1s} & P_{1u}\\ P_{2s} & P_{2u} \end{bmatrix}\begin{bmatrix}J_{s}P_{1s}^{-1}x_{t}^{1}-J_{s}P_{1s}^{-1}P_{1u}y_{t}^{u}\\ J_{u}y_{t}^{u} \end{bmatrix}+Bu_{t}\nonumber \\ & =\begin{bmatrix}P_{1s}J_{s}P_{1s}^{-1}x_{t}^{1}+(P_{1u}J_{u}-P_{1s}J_{s}P_{1s}^{-1}P_{1u})y_{t}^{u}\\ P_{2s}J_{s}P_{1s}^{-1}x_{t}^{1}+(P_{2u}J_{u}-P_{2s}J_{s}P_{1s}^{-1}P_{1u})y_{t}^{u} \end{bmatrix}+Bu_{t}.\tag{7.11} \end{align}\]

\(y_{t}^{u}\) は式(7.6) によって決定していることに注意せよ. なお, 式(7.11) には \(x^{2}\) が過去の情報に依存して決まっているという問題がある. \(x^{2}\) は初期条件が与えられない変数なので, 同時点の \(x^{1}\), \(u\) および未来の \(u\) にのみ依存する形で記述できなければならない.

少し計算を進めて Blanchard and Kahn (1980) の再帰公式 (p. 1308 (2), (3)式) を導出しよう. 彼らのモデルは確率的なモデルであるが, われわれの決定論モデルでも解の構造はまったく変わらない.

式(7.11) を使って, \(x_{t}^{1}\) を消去する. \(x_{t}^{1}\) の係数行列をそろえて

\[ \begin{aligned} P_{2s}P_{1s}^{-1}x_{t+1}^{1} & =P_{2s}J_{s}P_{1s}^{-1}x_{t}^{1}+(P_{2s}P_{1s}^{-1}P_{1u}J_{u}-P_{2s}J_{s}P_{1s}^{-1}P_{1u})y_{t}^{u}+P_{2s}P_{1s}^{-1}B_{1}u_{t}\\ x_{t+1}^{2} & =P_{2s}J_{s}P_{1s}^{-1}x_{t}^{1}+(P_{2u}J_{u}-P_{2s}J_{s}P_{1s}^{-1}P_{1u})y_{t}^{u}+B_{2}u_{t}, \end{aligned} \] これらの差を取る. \[ \begin{aligned} & x_{t+1}^{2}-P_{2s}P_{1s}^{-1}x_{t+1}^{1}\\ & =(P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})J_{u}y_{t}^{u}+(B_{2}-P_{2s}P_{1s}^{-1}B_{1})u_{t}\\ & =-(P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})J_{u}\sum_{k=0}^{\infty}J_{u}^{-k-1}C_{u}u_{t+k}+(B_{2}-P_{2s}P_{1s}^{-1}B_{1})u_{t}\\ & =-(P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})\sum_{k=0}^{\infty}J_{u}^{-k}C_{u}u_{t+k}+(B_{2}-P_{2s}P_{1s}^{-1}B_{1})u_{t}\\ & =-(P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})\left(C_{u}u_{t}+\sum_{k=0}^{\infty}J_{u}^{-k-1}C_{u}u_{t+k+1}\right)+(B_{2}-P_{2s}P_{1s}^{-1}B_{1})u_{t}\\ & =(P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})y_{t+1}^{u}. \end{aligned} \] 最後の等式には次の関係を使った. \[ (P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})C_{u}=B_{2}-P_{2s}P_{1s}^{-1}B_{1}. \] 定理としてまとめておこう.
定理 7.3 \(n_{1}=n_{s}\) かつ \(\det P_{1s}\neq0\) とする. このとき, (7.1) の解は一意に定まり, \(t=0,1,\dots\) について \(x_{t}\) は次式で与えられる. \[ \begin{aligned} x_{t+1}^{1} & =P_{1s}J_{s}P_{1s}^{-1}x_{t}^{1}+(P_{1u}J_{u}-P_{1s}J_{s}P_{1s}^{-1}P_{1u})y_{t}^{u} + B_1 u_t,\\ x_{t}^{2} & =P_{2s}P_{1s}^{-1}x_{t}^{1}+(P_{2u}-P_{2s}P_{1s}^{-1}P_{1u})y_{t}^{u},\\ y_{t}^{u} & =-\sum_{k=0}^{\infty}J_{u}^{-k-1}C_{u}u_{t+k},\\ x_{0}^{1} & :\ \text{given.} \end{aligned} \]

Blanchard and Kahn (1980) では再帰的でない解表現を得ているが, 単純な計算で導出できるのでここではあえて述べることはしない. 各自確認してほしい.

図解

2次元の場合に Blanchard-Kahn の定理を図解しよう.

図7.1 はジョルダン標準形に変換する前の座標系を表している. 初期時点 \(t=0\) で \(x\) が取りうる範囲は赤線で表された直線である. 1次元の自由度が与えられているのは, \(x_{0}^{1}\) が固定されている一方で, \(x_{0}^{2}\) が未知であることを反映している.

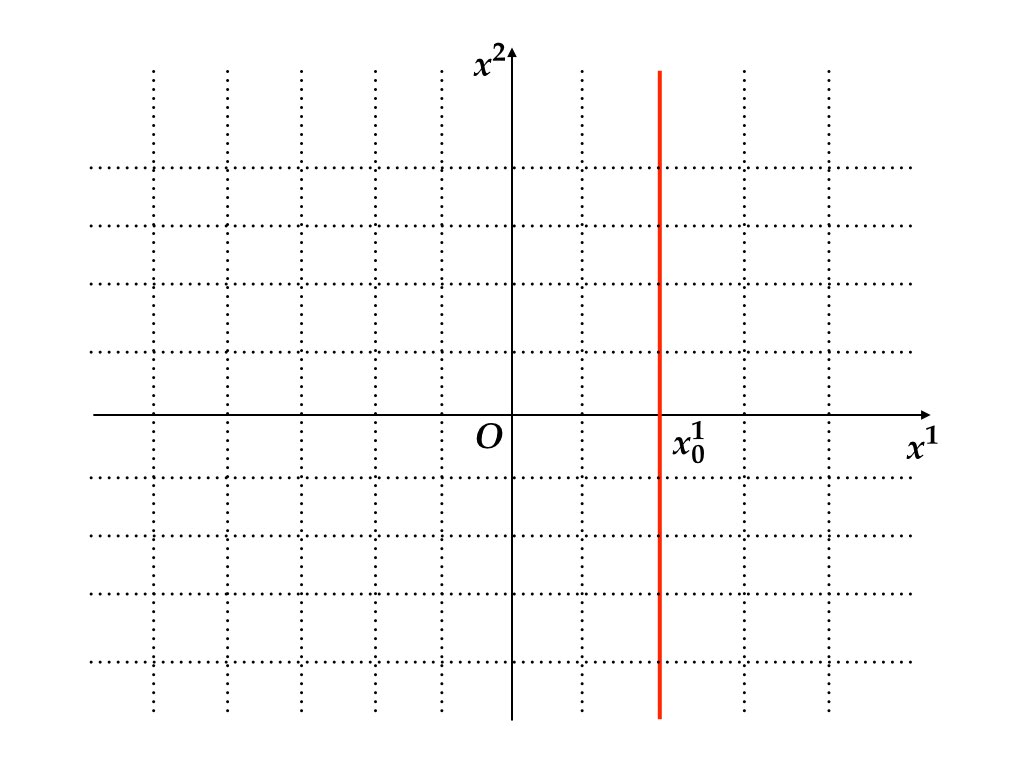
変換前の直交座標系. \(x_{0}^{1}\) だけが所与であり, \((x_{0}^{1},x_{0}^{2})\)は赤色実線上のどこかにある.

図 7.1: 変換前の直交座標系. \(x_{0}^{1}\) だけが所与であり, \((x_{0}^{1},x_{0}^{2})\)は赤色実線上のどこかにある.

図 7.2 はジョルダン標準形に変換した後の座標系である. すなわち, \(P=[P_{1}\ P_{2}]\) を基底とした座標系を表している. 一般に\(P\) は直交性を保たないので, 斜交座標系を描いている. 異なる座標系は同一の点を表現する別の方法を定めるだけであるから, \((x_{0}^{1},x_{0}^{2})\) の位置を表す赤色の直線は動かない. あくまで目盛りを変えただけである. 座標系の変更により \(y^{u}\) 軸に平行なサブシステム（不安定固有値に対応する固有空間上のシステム）と\(y^{s}\)軸に平行なサブシステム（安定固有値に対応する固有空間上のシステム）に分離することができる. 式 (7.4) を確認せよ.

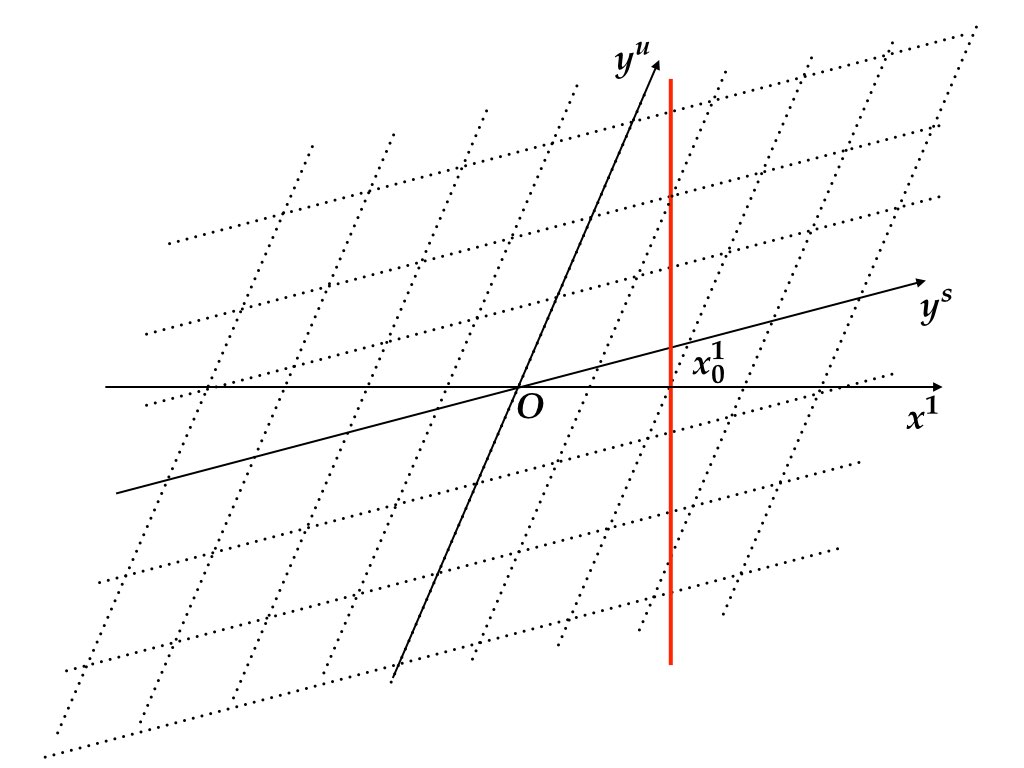
ジョルダン標準形に変換した後の斜交座標系. 座標系を変更しても赤色実線は動かない.

図 7.2: ジョルダン標準形に変換した後の斜交座標系. 座標系を変更しても赤色実線は動かない.

式 (7.6) は不安定固有値に対応する固有空間 (\(y_{u}\) 軸) に沿って後ろ向きに \(y_{0}^{u}\) を見つける手続きである. 将来にわたって \(u\) が決定していれば, \(t=\infty\) から \(t=0\) まで時間を逆向きに解いて \(y_{0}^{u}\) を決めることができる. この時点ではまだ \(y_{0}^{s}\) が決定しないので, \((y_{0}^{s},y_{0}^{u})\) は \((0,y_{0}^{u})\) を通り \(y^{s}\) 軸と平行な直線上にある. 図7.3 の青色実線を参照せよ. この直線は安定行列 \(J_{u}^{-1}\) によって特徴づけられる時間反転システムの極限を集めたものである.

直交座標の \((x_{0}^{1},x_{0}^{2})\) と斜交座標の\((y_{0}^{s},y_{0}^{u})\) が同じ点を表す場合に限り, それらは式(7.1) の\(t=0\) における値として適切に選ばれていると言ってよい. 一方を他方の座標系で表して一致することを確かめればよいので, 式(7.8), (7.9) を解けばよいことが分かるだろう. もちろんこれは (7.10) と同値である. 解の一意決定性のための条件は, 赤線と青線の交点が一意に存在するための条件に外ならない (図???). なお, \(P_{1s}\) の正則性は赤色の実線と青色の実線が平行にならないことを保証している.

安定な後ろ向き (forward-looking) サブシステム \(y_{t}^{u}=J_{u}^{-1}y_{t+1}^{u}-J_{u}^{-1}C_{u}u_{t}\) の 極限 (\(t=0\))で \(y_{0}^{u}\) が決まる.

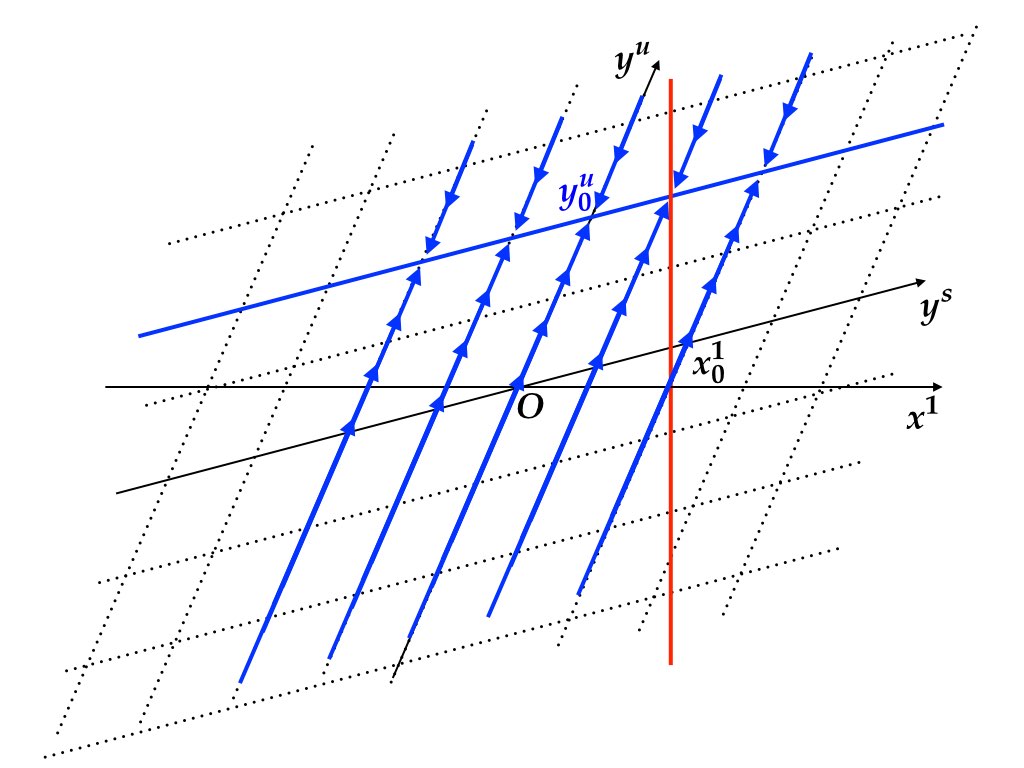
図 7.3: 安定な後ろ向き (forward-looking) サブシステム \(y_{t}^{u}=J_{u}^{-1}y_{t+1}^{u}-J_{u}^{-1}C_{u}u_{t}\) の 極限 (\(t=0\))で \(y_{0}^{u}\) が決まる.

青色と赤色の直線が交わる点で \((x_{0}^{1},x_{0}^{2})\) あるいは \((y_{0}^{s},y_{0}^{u})\) が定まる.

図 7.4: 青色と赤色の直線が交わる点で \((x_{0}^{1},x_{0}^{2})\) あるいは \((y_{0}^{s},y_{0}^{u})\) が定まる.

\((y_{0}^{s},y_{0}^{u})\) あるいは \((x_{0}^{1},x_{0}^{2})\) が定まれば, 式(7.1) を繰り返し適用することで解軌道を決定できる.

最後に, 解が存在しないケースと不決定の場合について述べる. まず, 固有値が2つとも不安定固有値である場合, すなわち \(n_{u}=n=2\), \(0=n_{s}<n_{1}=1\) のケースを考えよう. 図7.5 で示されている通り, 後ろ向き (forward-looking) サブシステム \(y_{t}^{u}=J_{u}^{-1}y_{t+1}^{u}-J_{u}^{-1}C_{u}u_{t}\) は一点 \((y_{0}^{u1},y_{0}^{u2})\) を定める. 赤色の実線と一般には交わらないので, 解が存在しない. 次に　\(n_{u}=0\), \(2=n_{s}>n_{1}=1\) のケースを考える. この場合には後ろ向きのサブシステムはないので, \(y_{0}\) に関して情報を得ることができない. したがって, 2次元平面\((y^{s1},y^{s2})\)のすべての点が \((y_{0}^{s1},y_{0}^{s2})\) の候補となる (図 7.6). 青色領域と赤色直線が交わる点は1次元の自由度を持つ無限個の点の集まりであるから \(x_{0}^{2}\) を定めることもできない.

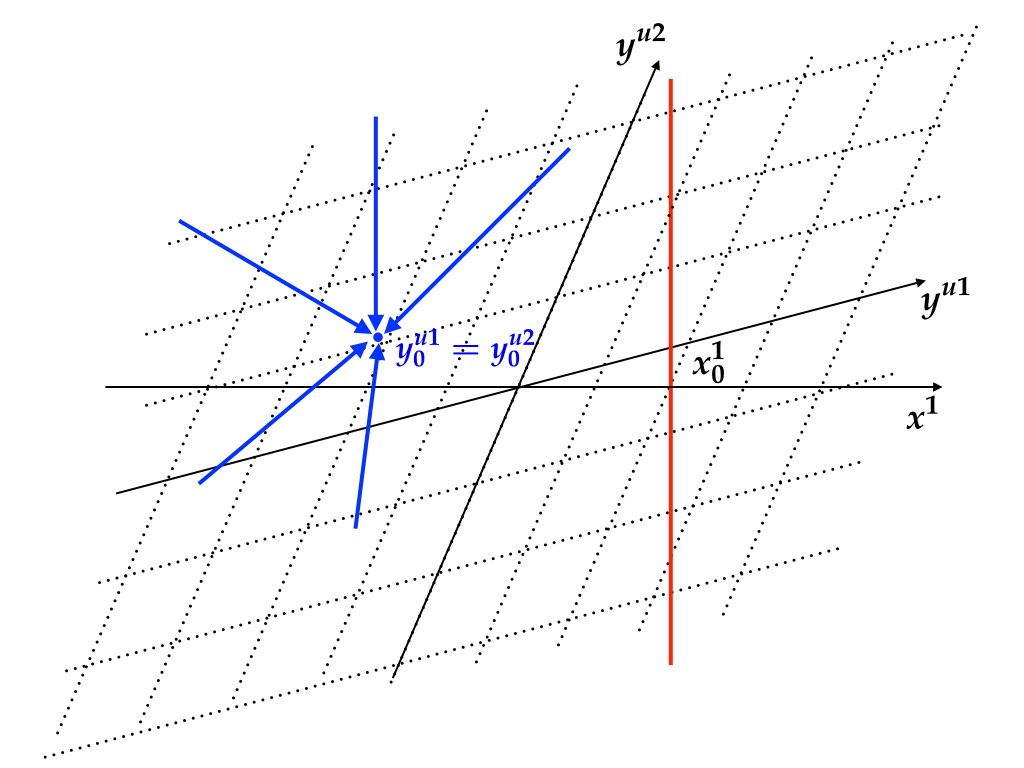
\(n_{s}<n_{1}\) のケース. バックワードサブシステムが過剰に初期値を定めてしまう. 一般に解は存在しない.

図 7.5: \(n_{s}<n_{1}\) のケース. バックワードサブシステムが過剰に初期値を定めてしまう. 一般に解は存在しない.

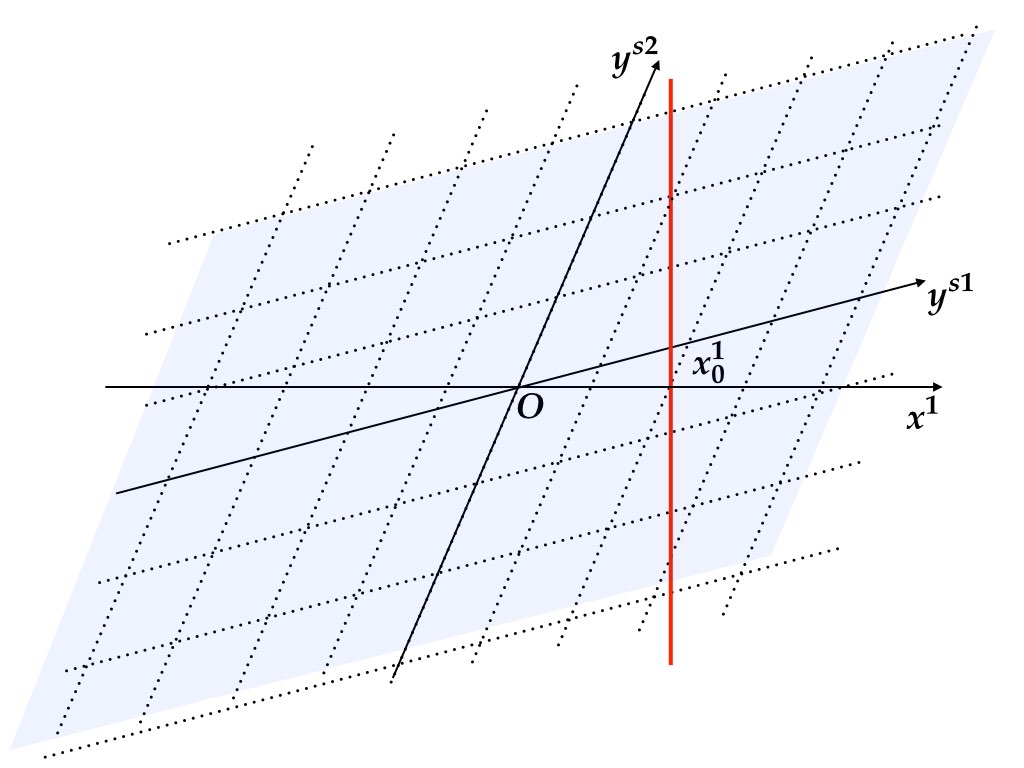
\(n_{s}>n_{1}\) のケース. バックワードサブシステムの情報が不足しており, 赤色直線上の任意の点から出発した経路が解の性質を満たす.

図 7.6: \(n_{s}>n_{1}\) のケース. バックワードサブシステムの情報が不足しており, 赤色直線上の任意の点から出発した経路が解の性質を満たす.

7.3 \(E \neq I\) のケース

7.3.1 アイデア

次にシステム方程式がデスクリプタ方程式

\[ Ex_{t+1}=Ax_{t}+Bu_{t},\quad t=0,1,\dots,\tag{7.12} \] で与えられている場合の解を求めよう. 前節と同様に, 初期時点における変数 \[ x_{0}=\begin{bmatrix}x_{0}^{1}\\ x_{0}^{2} \end{bmatrix}\in\mathbb{R}^{n_{1}}\times\mathbb{R}^{n_{2}} \] について \(x_{0}^{1}=\bar{x}_{0}^{1}\in\mathbb{R}^{n_{1}}\) のみ拘束条件が与えられているとする.

\(E=I\) のケースでは \(A\) のジョルダン標準形を求めることで解を計算したが, \(E\neq I\) の場合, 特に \(\det E\neq0\) の場合には\((E,A)\) のワイエルシュトラス標準形によって解を特徴付ける. 資料 {[}16ED04{]} で見たとおり, 適当な正則行列 \(V,W\) が存在して, \[\begin{align} W^{-1}EV & =\begin{bmatrix}I\\ & N \end{bmatrix},\tag{7.13}\\ W^{-1}AV & =\begin{bmatrix}J\\ & I \end{bmatrix},\tag{7.14} \end{align}\] が成り立つ . ここで, \(J\) は\((E,A)\) の有限固有値を対角成分にもつジョルダン標準形行列, \(N\) は対角成分がすべてゼロであるジョルダン標準形行列である. もちろん \(\det E\neq0\) であれば, \(N\) は現れない. ここで, \(J\) は \[\begin{equation} J=\begin{bmatrix}J_{fs}\\ & J_{fu} \end{bmatrix}\tag{7.15} \end{equation}\]

というブロックに分かれており, \(J_{fs}\) の対角成分に絶対値が1以下の一般固有値, \(J_{fu}\)の対角成分に絶対値が1未満の一般固有値が並ぶようにする. \(V\), \(W\) の選び方は {[}16ED04{]} で解説した通りである. \(V\) は一般化固有ベクトルを並べたもの, \(W\) はそれに \((E,A)\) を掛けたものであるから, ベクトルの並びによって固有値の順序を自由に設定できる.

変数変換 \(y=V^{-1}x\), 変数の分割 \(y=(y^{fs},y^{fu},y^{b})\in\mathbb{R}^{n_{fs}}\times\mathbb{R}^{n_{fu}}\times\mathbb{R}^{n_{b}}\), \(W^{-1}B=(C_{fs},C_{fu},C_{b})\) を施して \[ \begin{bmatrix}I_{n_{fs}}\\ & I_{n_{fu}}\\ & & N \end{bmatrix}\begin{bmatrix}y_{t+1}^{fs}\\ y_{t+1}^{fu}\\ y_{t+1}^{b} \end{bmatrix}=\begin{bmatrix}J_{fs}\\ & J_{fu}\\ & & I \end{bmatrix}\begin{bmatrix}y_{t}^{fs}\\ y_{t}^{fu}\\ y_{t}^{b} \end{bmatrix}+\begin{bmatrix}C_{fs}\\ C_{fu}\\ C_{b} \end{bmatrix}u_{t}. \] を得る. このシステムを以下のように2つのサブシステムに分解する. \[\begin{align} y_{t+1}^{fs} & =J_{fs}y_{t}^{fs}+C_{fs}u_{t}\tag{7.16}\\ \begin{bmatrix}y_{t}^{fu}\\ y_{t}^{b} \end{bmatrix} & =\begin{bmatrix}J_{fu}^{-1}\\ & N \end{bmatrix}\begin{bmatrix}y_{t+1}^{fu}\\ y_{t+1}^{b} \end{bmatrix}-\begin{bmatrix}J_{fu}^{-1}C_{fu}\\ C_{b} \end{bmatrix}u_{t}\tag{7.17}\\ & =:\hat{J}_{u}y_{t+1}^{u}-D_{u}u_{t}. \end{align}\]

{[}16ED04{]} の場合と異なり, 式 (7.17) が不安定な有限固有値に対応するサブシステムを時間反転して付加していることに注意してほしい. \((E,A)\) の有限不安定固有値と無限大固有値をいずれも不安定固有値とみなすならば, 前節の結果を応用すれば解軌道が求まることも想像に難くないだろう. ただし, \(N\) の非正則性に伴うデリケートな問題が生じることに注意をしておこう. システム(7.1) では, 初期値を定めるために後ろ向きのシステムを作ったが, あくまでも順方向に決定されるシステムであり, 再帰的な構造を見つけることができた. しかし, システム (7.12) には無限大固有値に対応する本質的に非因果的な成分が含まれるので, \(\det E=0\) である場合, 一般には再帰的に (因果的に) 記述できるとは限らない.

7.3.2 解の存在と一意性

まずは, 式 (7.17) を解いてみよう. \[\begin{align} y_{t}^{fu} & =-\sum_{k=0}^{\infty}J_{fu}^{-k-1}C_{fu}u_{t+k},\tag{7.18}\\ y_{t}^{b} & =N\left(Ny_{t+2}^{b}-C_{b}u_{t+1}\right)-C_{b}u_{t}\nonumber \\ & =N^{n_{b}}y_{t+n_{b}}^{b}-\sum_{k=0}^{n_{b}-1}N^{k}C_{b}u_{t+k}\nonumber \\ & =-\sum_{k=0}^{n_{b}-1}N^{k}C_{b}u_{t+k}.\tag{7.19} \end{align}\] ここでも, \(\lim_{T}\|J_{fu}^{-T}C_{fu}u_{T}\|=0\) と \(y_{t}^{fu}\) に現れる級数の収束性が成り立つように \(u_{t}\) を制限しているものとする. 初期時点の変数を決定する線形方程式は次式で与えられる. \[\begin{align} \begin{bmatrix}\bar{x}_{0}^{1}\\ x_{0}^{2} \end{bmatrix} & =\left[\begin{array}{c|cc} V_{1fs} & V_{1fu} & V_{1b}\\ \hline V_{2fs} & V_{2fu} & V_{2b} \end{array}\right]\left[\begin{array}{c} y_{0}^{fs}\\ \hline \bar{y}_{0}^{fu}\\ \bar{y}_{0}^{b} \end{array}\right].\tag{7.20}\\ & =:\left[\begin{array}{c|c} V_{1fs} & V_{1u}\\ \hline V_{2fs} & V_{2u} \end{array}\right]\begin{bmatrix}y_{0}^{fs}\\ \bar{y}_{0}^{u} \end{bmatrix} \end{align}\] すでに決定している変数には上線を付している. 第7.2節のケースと同様に式(7.20)を \((y_{0}^{fs},x_{0}^{2})\) について解くことができれば解軌道の存在が示される. 未知変数を左辺に集めると, \[\begin{equation} \begin{bmatrix}V_{1fs} & 0\\ V_{2fs} & -I \end{bmatrix}\begin{bmatrix}y_{0}^{fs}\\ x_{0}^{2} \end{bmatrix}=\begin{bmatrix}I & -V_{1fu} & -V_{1b}\\ 0 & -V_{2fu} & -V_{2b} \end{bmatrix}\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{fu}\\ \bar{y}_{0}^{b} \end{bmatrix}=\begin{bmatrix}I & -V_{1u}\\ 0 & -V_{2u} \end{bmatrix}\begin{bmatrix}\bar{x}_{0}^{1}\\ \bar{y}_{0}^{u} \end{bmatrix}\tag{7.21} \end{equation}\]

が得られる. 式(7.20) から (7.21) は \(t=0\) について記述しているが, \(t=0\) 以外の時点でも同様に成り立つことに注意せよ.

定理 7.3 の拡張となる次の結果を得る.
定理 7.4 システム (7.12) に関して, \(n_{1}=n_{fs}\) かつ \(\det V_{1fs}\neq0\) が成り立てば, \((y_{0}^{fs},x_{0}^{2})\) および解が一意的に定まる.

式 (7.21) を用いて, 解の不存在および不決定性が起こる場合の議論を完成させなさい.

ここで得られた結果は, 有限不安定固有値と無限大固有値の区別に依存していないことに注意せよ. 無限大固有値を不安定固有値とみなせば Blanchard-Kahn の定理7.3 の条件とまったく同じものと言ってよい. ただし, 解公式は同じにはならない. 前節の \(J_{u}^{-1}\) は可逆 (これは当たり前のことである) であったのに対して, \(\det E=0\) の場合 \(\hat{J}_{u}\) は可逆ではない. したがって, 前節とは違って後ろ向きの方程式に対応する順方向の方程式は存在せず, 定理 7.3 の公式は適用できない.

7.3.3 \(u\) の特定化

一般の \(u\) について解を特徴付けようとするとかなり煩雑になるので, Klein (2000) に倣って \(u\) に強い条件を課した上で再帰公式を求めよう. Klein (2000) では \(u\) が状態方程式 \[ u_{t+1}=\Phi u_{t},\quad\Phi\in\mathbb{R}^{m\times m},\quad u_{0}:\text{ given} \]

に従うと仮定する.28 式 (7.18), (7.19) を次のように書き換えておく.29

\[ y_{t}^{u}=-\sum_{k=0}^{\infty}\hat{J}_{u}^{k}D_{u}u_{t+k}. \] \(u\) に対する仮定から\(u_{t+k}=\Phi^{k}u_{t}\), \(k=0,1,\dots\), が成り立つので, \[ \begin{aligned} y_{t}^{u} & =-\left(\sum_{k=0}^{\infty}\hat{J}_{u}^{k}D_{u}\Phi^{k}\right)u_{t}.\\ & =:Mu_{t}. \end{aligned} \] 行列\(M\)を計算しよう. 簡単な計算から \[ M =-\left(\sum_{k=0}^{\infty}\hat{J}_{u}^{k}D_{u}\Phi^{k}\right) =-D_{u}-\sum_{k=1}^{\infty}\hat{J}_{u}^{k}D_{u}\Phi^{k} =-D_{u}+\hat{J}_{u}M\Phi \]

が得られ, \(M\) は離散時間シルベスタ方程式の解であることが分かる. 定理 7.2 より, \[ \mathrm{vec}(M)=\left[\left(\Phi^{\top}\otimes\hat{J}_{u}\right)-I\right]^{-1}\mathrm{vec}(D_{u}). \]

さらに計算を進めよう.

\[ \begin{aligned} \begin{bmatrix}x_{t+1}^{1}\\ x_{t+1}^{2} \end{bmatrix} & =\begin{bmatrix}V_{1fs} & V_{1u}\\ V_{2fs} & V_{2u} \end{bmatrix}\begin{bmatrix}y_{t+1}^{fs}\\ y_{t+1}^{u} \end{bmatrix}\\ & =\begin{bmatrix}V_{1fs} & V_{1u}\\ V_{2fs} & V_{2u} \end{bmatrix}\begin{bmatrix}J_{fs}y_{t}^{fs}+C_{fs}u_{t}\\ Mu_{t+1} \end{bmatrix}\\ & =\begin{bmatrix}V_{1fs} & V_{1u}\\ V_{2fs} & V_{2u} \end{bmatrix}\begin{bmatrix}J_{fs}V_{1fs}^{-1}\left(x_{t}^{1}-V_{1u}y_{t}^{u}\right)+C_{fs}u_{t}\\ Mu_{t+1} \end{bmatrix}\\ & =\begin{bmatrix}V_{1fs} & V_{1u}\\ V_{2fs} & V_{2u} \end{bmatrix}\begin{bmatrix}J_{fs}V_{1fs}^{-1}x_{t}^{1}+(C_{fs}-J_{fs}V_{1fs}^{-1}V_{1u}M)u_{t}\\ Mu_{t+1} \end{bmatrix}. \end{aligned} \]

\(x_{t+1}^{2}\) には\(t\) 期以前の情報が入ってほしくないので, 前節と同様に過去の情報を消去する.

\[ \begin{aligned} V_{2fs}V_{1fs}^{-1}x_{t+1}^{1} & =V_{2fs}J_{fs}V_{1fs}^{-1}x_{t}^{1}+V_{2fs}(C_{fs}-J_{fs}V_{1fs}^{-1}V_{1u}M)u_{t}+V_{2fs}V_{1fs}^{-1}V_{1u}Mu_{t+1}\\ x_{t+1}^{2} & =V_{2fs}J_{fs}V_{1fs}^{-1}x_{t}^{1}+V_{2fs}(C_{fs}-J_{fs}V_{1fs}^{-1}V_{1u}M)u_{t}+V_{2u}Mu_{t+1}. \end{aligned} \] 上式から下式を引いて \[ V_{2fs}V_{1fs}^{-1}x_{t+1}^{1}-x_{t+1}^{2}=\left(V_{2fs}V_{1fs}^{-1}V_{1u}-V_{2u}\right)Mu_{t+1} \]

を得る. これを \(x_{t+1}^{2}\) について解けばよい. したがって, \[ \begin{aligned} x_{t+1}^{1} & =V_{1fs}J_{fs}V_{1fs}^{-1}x_{t}^{1}+\left[V_{1fs}C_{fs}-V_{1fs}J_{fs}V_{1fs}^{-1}V_{1u}M+V_{1u}M\Phi\right]u_{t}\\ x_{t}^{2} & =V_{2fs}V_{1fs}^{-1}x_{t}^{1}+\left(V_{2u}-V_{2fs}V_{1fs}^{-1}V_{1u}\right)Mu_{t}. \end{aligned} \] 随所に \(u_{t+1}=\Phi u_{t}\) を用いている. 定理としてまとめよう.

定理 7.5 \(n_{1}=n_{fs}\) かつ \(\det V_{1fs}\neq0\) とする. このとき, (7.12) の解は一意に定まる. 外生変数 が \(u_{t+1}=\Phi u_{t}\) に従うとすれば, \(x_{t}\), \(t=0,1,\dots\) , は次式で与えられる. \[ \begin{aligned} x_{t+1}^{1} & = V_{1fs}J_{fs}V_{1fs}^{-1}x_{t}^{1} + \left[ V_{1fs}C_{fs}-V_{1fs}J_{fs}V_{1fs}^{-1}V_{1u}M + V_{1u}M\Phi \right] u_{t} \\ x_{t}^{2} & = V_{2fs}V_{1fs}^{-1}x_{t}^{1} + \left( V_{2u}-V_{2fs}V_{1fs}^{-1}V_{1u} \right) Mu_{t}.\\ x_{0}^{1} & :\ \text{given}. \end{aligned} \] ただし\(M\)は \[ \mathrm{vec}(M)=\left[\left(\Phi^{\top}\otimes\hat{J}_{u}\right)-I\right]^{-1}\mathrm{vec}\left(D_{u}\right) \] によって決まる行列.

定理 7.3 において \(u_{t+1}=\Phi u_{t}\) を仮定したときの解の公式を導出せよ.

参考文献

Blanchard, Olivier Jean, and Charles M. Kahn. 1980. “The Solution of Linear Difference Models Under Rational Expectations.” Econometrica 48 (5): 1305–12.

Klein, Paul. 2000. “Using the Generalized Schur Form to Solve a Multivariate Linear Rational Expectations Model.” Journal of Economic Dynamics & Control 24: 1405–23.

  1. Klein (2000) はQZ分解を用いた解法を提案している. 理論的にはワイエルシュトラス標準形を使う方が綺麗な結果が得られるので, Klein (2000) の方針に沿った上でワイエルシュトラス標準形を使って書き直している.↩

  2. 経済学で forward というと「未来から現在に向かって」という意味で使われるようである. すなわち, 観察している情報が未来（前方）にあることを意識している. しかし, 数学その他の分野で forward というと「現在から過去に向かって」という風に時間がどちらに流れているかを意識して使われるようである. 大変ややこしいが, 本稿では forward というときには「現在から過去に向かって」という意味で「時間の流れ」を意識する数学流の意味とし, 観測している情報が前方にあることを意図する経済学的な forward に対しては forward-looking という形容詞を使って区別する. backward, backward-looking, あるいは日本語の前向き, 後ろ向きについても同様である.↩

  3. \(u_{t+k}\) の極限での振る舞いにも仮定を置かなければこの級数が収束しないかもしれない. 簡単のため級数の収束性を保証する条件が置かれているものとしよう.↩

  4. Klein (2000) は確率的なモデルを扱っているが, ここでの取り扱いと実質的には変わらない.↩

  5. この変形により \(y_{t}^{b}\) は有限期先の未来にしか依存しないという情報を捨てている.↩